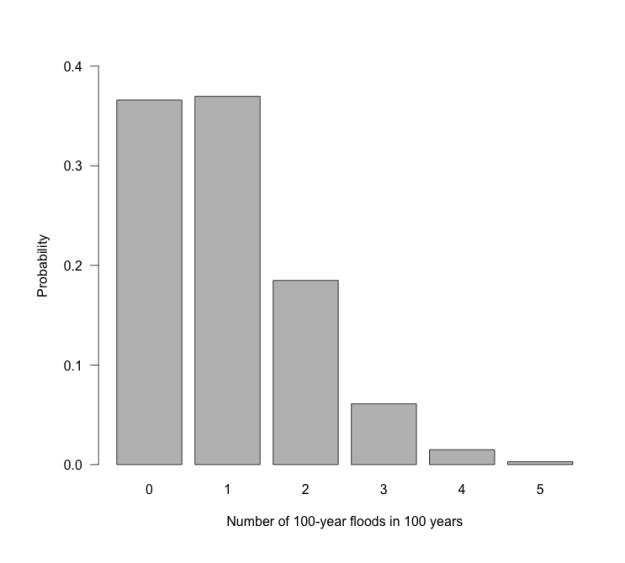
I previously wrote about considering the occurrence of 1% floods as a binomial distribution, this post extends that analysis to look at conditional probabilities. Some of the results are counter intuitive, at least to me, in that the risk of multiple 1% floods is larger than I would have guessed.
The probability of a 1% (1 in 100) annual exceedance probability (AEP) flood occurring in any year is 1%. This can be treated as the probability of a “success” in the binomial distribution, with the number of trials being the number of years. So the probability of having exactly one 1% flood in 100 years is
In R this can be calculated as dbinom(x = 1, size = 100, prob = 0.01) or in excel =BINOM.DIST(1,100, 0.01, FALSE).
The cumulative distribution function of the binomial distribution is also useful for flood calculations.
What is the probability of 2 or more 1% floods in 100 years:
R: pbinom(q = 1, size = 100, prob = 0.01, lower.tail = FALSE) = 0.264
Excel: =1 - BINOM.DIST(1,100, 0.01, TRUE) = 0.264
We can check this by calculating the probability of zero or one flood in 100 years and subtracting that value from 1.
1 - (dbinom(x = 1, size = 100, prob = 0.01) + dbinom(x = 0, size = 100, prob = 0.01)) = 0.264
We can also do conditional probability calculations which could be useful for risk assessment scenarios.
What is the probability that exactly two 1% floods occur in 100 years given that at least one occurs?
dbinom(x = 2, size = 100, prob = 0.01)/pbinom(q = 0, size = 100, prob = 0.01, lower.tail = FALSE) = 0.291
What is the probability that at least two 1% floods occur in 100 years given that at least one occurs?
pbinom(q = 1, size = 100, prob = 0.01, lower.tail = FALSE)/pbinom(q = 0, size = 100, prob = 0.01, lower.tail = FALSE) = 0.416
We can also check this by simulation. This code generates the number of 1% floods in each of 100,000 100-year sequences. We can then count the number of interest.
set.seed(1969) # use a random number seed so the analysis can be repeated if necessary floods = rbinom(100000,100, 0.01) # generate the number of 1% floods in each of 100,000, 100-year sequences floods_subset = floods[floods >= 1] # Subset of sequences that have 1 or more floods # Number of times there are two or more floods in the subset of 1 or more floods sum(floods_subset >= 2) / length(floods_subset) # 0.4167966 # or sum(floods >= 2)/sum(floods >= 1) #[1] 0.4167966
A slightly tricker situation is a question like: What is the probability of three or fewer floods in 100-years given there is more than one.
floods_subset = floods[floods > 1] # Subset of sequences that have more than one flood # Number of times there are three or fewer floods in the subset of more than one flood sum(floods_subset ≤ 3) / length(floods_subset) #[1] 0.9310957 # Or, for the exact value # (Probability that X = 3 + Probability that X = 2)/(Probability that X > 1) (dbinom(x = 3, size = 100, prob = 0.01) + dbinom(x = 2, size = 100, prob = 0.01))/ pbinom(q = 1, size = 100, prob = 0.01, lower.tail = FALSE) #[1] 0.9304641
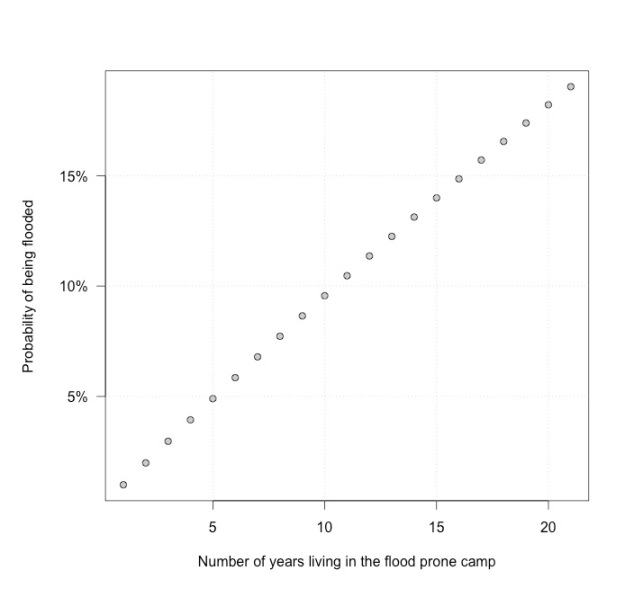
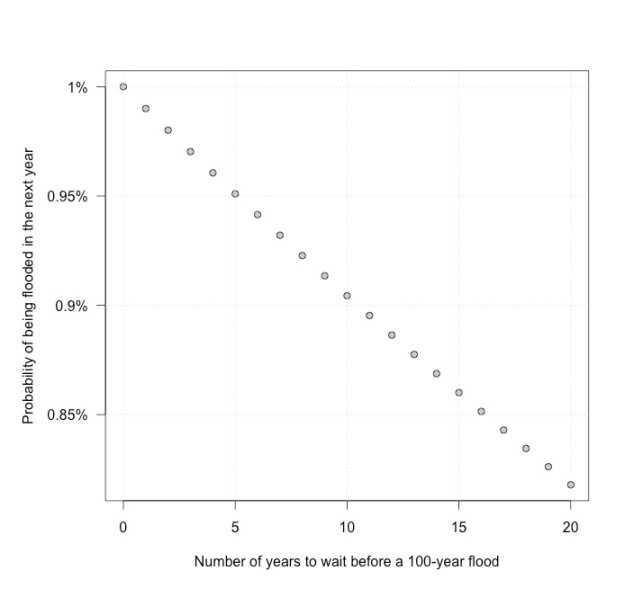
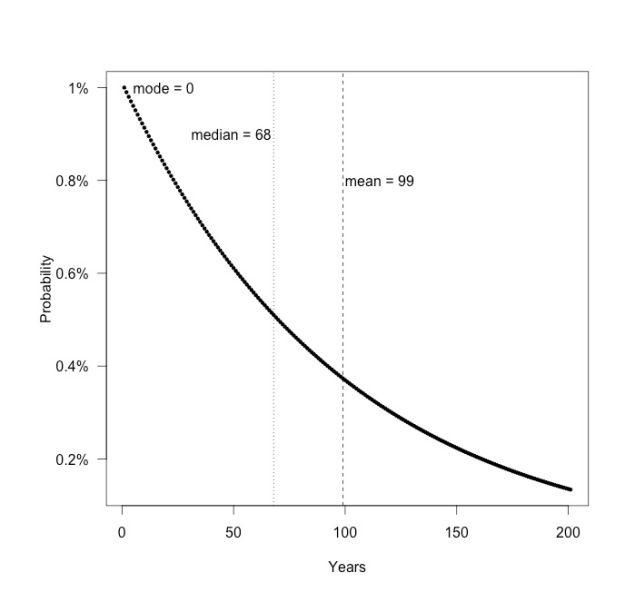
The probability of experiencing at least one 1% flood in 100-years is 
We can also solve this numerically. In R the formula is 0.99 = pbinom(q=0, size = n, prob = 0.01), solve for n. Using the uniroot function gives n = 459 years (see below).
So all these areas subject to a 1% flood risk will flood eventually, but it may take a while.
f = function(n) {
n = as.integer(n) #n must be an integer
0.99 - pbinom(q = 0, size = n, prob = 0.01, lower.tail = FALSE)
}
# $root
# [1] 458.4999
uniroot(f, lower = 100, upper = 1000)
pbinom(q = 0, size = 459, prob = 0.01, lower.tail = FALSE)
# [1] 0.990079
How many years before there is a >99% chance of experiencing more than one flood? This is one minus (the probability of zero floods + the probability of one flood).
Let the number of years equal n.
or 18.5%
tonyladson 