Routing in RORB

1 Reply

I’ve been reviewing some of the background that explains the way RORB works, particularly Appendix A in the RORB manual and the 1974 paper by Mein, Laurenson and McMahon Simple Nonlinear Model for Flood Estimation.

The key mathematical aspects of RORB are the continuity equation and a relationship between storage and discharge.

For any storage, the continuity equation can be written as: “inflow in a time period, minus outflow in that time period equals change in storage”.

Or as used in RORB:

\frac{I_t+I_{t+1}}{2}-\frac{Q_t+Q_{t+1}}{2} = \frac{S_{t+1}-S_t}{\Delta t}        (1)

Where I is inflow, Q is outflow, S is storage and \Delta t is the time step, t is one time period and t+1 is the next time period.

The relationship between storage and discharge used in RORB is:

S = kQ^m        (2)

This is justified in Appendix A of the RORB manual and in Mein et al. (1974).

Substituting equation (2) into (1):

\frac{I_t+I_{t+1}}{2} + \frac{Q_t+Q_{t+1}}{2} = \frac{kQ_{t+1}^m-kQ_t^m}{\Delta t}        (3)

In the general case, we are solving for the outflow Q_{t+1} and know all the other parameters i.e. the inflow (I_t and I_{t+1}), the outflow at the previous time step Q_t, along with m and k which are properties of a catchment and/or a waterway.

Equation (3) can be rearranged as follows

Q_t + Q_{t+1} - I_t - I_{t+1} + \frac{2k}{\Delta t} \left( Q_{t+1}^m-Q_t^m \right) = 0        (4)

I’ve written that equation (4) is equal to zero, but this will only be the case if we have the correct value of Q_{t+1}.

This opens the possibility of a numerical solution; guess a value of Q_{t+1} and plug it into equation (4), if that doesn’t equal zero,  guess again. In applied mathematics, this is referred to as root finding i.e. finding where a function equals zero. There are a number of procedures to do this efficiently (see for example, Numerical Recipes).

Let’s start with the Newton-Raphson procedure which the method discussed in Mein et al. (1974)

Think of equation (4) as a function of Q_{t+1} i.e.

f \left( Q_{t+1}\right) = Q_t + Q_{t+1} - I_t - I_{t+1} + \frac{2k}{\Delta t} \left( Q_{t+1}^m-Q_t^m \right)      (5)

We guess a value of Q_{t+1} say Q_{t+1.1} and would like to calculate a better guess that brings f \left( Q_{t+1}\right) closer to zero. Consider the derivative of f \left( Q_{t+1}\right) at our initial guess, this is just the slope of the tangent at Q_{t+1.1} as shown in the figure below which hits the axes at a point closer to the required root so would be a good next guess.  Call this pointQ_{t+1.2} .

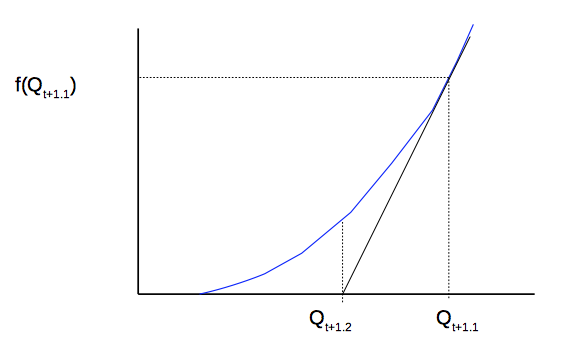
Newton

The slope is rise/run so in this case.

f' \left( Q_{t+1}\right) = \frac{ f \left( Q_{t+1}\right)}{Q_{t+1.1} - Q_{t+1.2}}        (6)

Now, rearrange (6) to give an expression for Q_{t+1.2}

Q_{t+1.2} = Q_{t+1.1} - \frac{f \left( Q_{t+1}\right)}{f' \left( Q_{t+1}\right)}      (7)

Next we need the derivative of equation (5) with respect to Q_{t+1}

f' = 1 + \frac{2km}{\Delta t}Q^{m-1}_{t+1}       (8)

Using this approach to find Q_{t+1.2}, substitute (8) and (5) into (7) to give.

Q_{t+1.2} = Q_{t+1.1} - \frac{\Delta t \left(Q_{t+1.1} + Q_t - I_{t+1} - I_t \right) +2k \left( Q^m_{t+1.1} - Q^m_t \right)}{\Delta t + 2kmQ^{m-1}_{t+1.1}}       (9)

Equation (9) is the same as equation (8) in Mein et al. (1974).

The iterative solution proceeds as follows.

  1. Select an initial value of Q for the first timestep Q _{t},
  2. Guess Q _{t+1.1} (Mein et al. use (I_{t+1} + Q_t)/2
  3. Use equation (9) to calculate Q_{t+1.2}
  4. Set Q_{t+1.1} = Q_{t+1.2}
  5. Calculate a new Q_{t+1.2}
  6. Repeat steps 3 to 5 until Q_{t+1.2} has a similar value to Q_{t+1.1} or, equivalently, until equation (4) does in fact equal zero (or is nearly equal to zero).
  7. Go to the next timestep
  8. Set Q _{t} (current timestep) equal to  Q_{t+1} (from the previous timestep)
  9. Repeat steps 2 to 8 for all time steps

This sounds straightforward but there can be numerical issues.  The initial guess needs to be quite close to the answer or the next guess provided by equation (9) could be a negative flow.  Putting this back into equation (5) will cause an error because it requires raising a negative number to a fractional power. Another challenge is that the derivative (equation 8) is undefined when Q^m_{t+1} is zero if m < 1.

When reading the RORB manual, section 2.2.5 there is a comment that: “The Regular Falsi convergence algorithm was used”.  There is a good description of this root finding approach in Wikipedia.  The upshot is that RORB does not use Newton-Raphson as was discussed in Mein et al. 1974.

In R, the uniroot function provides a reliable way of root finding without the numerical issues of the Newton-Raphson procedure. uniroot is based on a C function zeroin as documented here.

A simple routing function, in R, is below.

Routing <- function(Ihydrograph, k, m, T, dt = 1, plotit = TRUE, return.values = FALSE){

# Ihydrograph is a function that describes the inflow hydrograph
# k and m are the routing parameters
# dt is the time step

 I <- rep(0, T+1) # Initialise input vector
 Q <- rep(0, T+1) # Initialise output vector
 S <- rep(0, T+1) # Initialise storage vector
 
 
 I[1] <- Ihydrograph(1) # initialise inflow

 # Continuity equation that we seek to set to zero to determine Q at the next time step

 myF <- function(Qip1, Qi, Ii, Iip1, k, m, dt){
 
 Qip1 + Qi - Iip1 - Ii + (2*k/dt)*(Qip1^m - Qi^m)
 
 }


 for(i in 1:100){
 I[i+1] <- Ihydrograph(i+1)
 Q[i+1] <- uniroot(myF, interval = c(0,10), Qi = Q[i], Ii = I[i], Iip1 = I[i+1], k, m, dt)$root
 S[i+1] <- k*Q[i+1]^m
 
 }
 
 
 if(plotit){
 plot(I, type = 'l', col = 'blue', las = 1, ylab = 'flow', xlab = 'Time step') # Inflow hydrograph
 lines(Q) # outflow hydrograph
 legend('topright', legend = c('Inflow', 'Outflow'), lty = 1, col = c('blue', 'black'), bty = 'n' )
 }
 
 if(return.values) return(Q)

}

Let’s test it using a hydrograph as a function (see this blog for details).
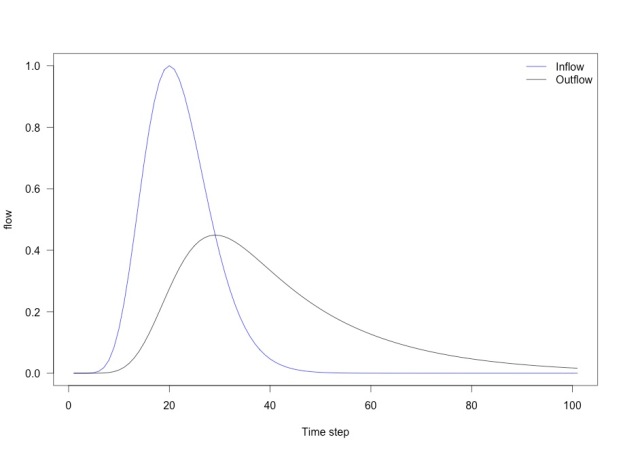
Routing1

What about the influence of k  on routing?

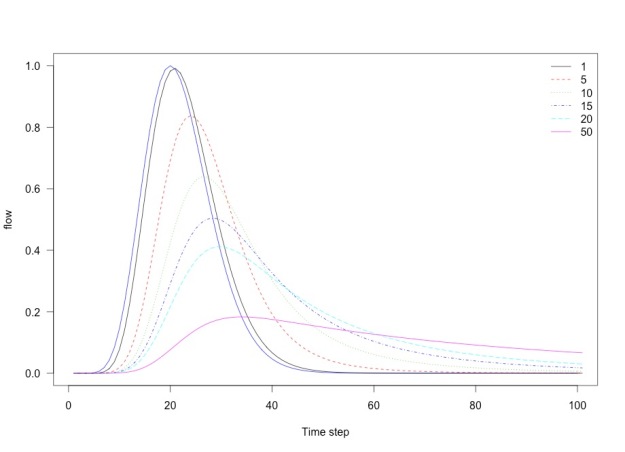
Routing_k.jpeg

Influence of the k parameter on routing

RORB starts with a rainfall excess hyetograph (the rainfall that is left over after losses have been subtracted) and then routes this through a series of elements to produce flow at the catchment outlet.  Here I’ve modelled a single element but that gives an indication of how the program works.

Code for the routing function and to produce these figures (also available as a gist).

Code to produce these figures.
# Specify an inflow hydrograph as a function
# See https://tonyladson.wordpress.com/2015/07/21/hydrograph-as-a-function/

my.Qmin <- 0
my.Qmax <- 1
my.beta <- 10
my.t.peak <- 20

Hydro <- function(tt, t.peak = 3, Qmin = 1, Qmax = 2, beta = 5) {
Qmin + (Qmax - Qmin)*( (tt/t.peak) * (exp(1 - tt/t.peak)))^beta

}
# Initialise the inflow
Ihydrograph <- function(tt){
Hydro(tt, t.peak = my.t.peak, Qmin = my.Qmin, Qmax = my.Qmax, beta = my.beta)
}

# Routing
Routing(Ihydrograph, k = 20, m = 1, T = 100, plotit = TRUE, return.values = FALSE)
# Step function hydrograph (or possibly based on measured inflows)

inflow <- c(0,0, 1,1,1,1,1, rep(0, times = 94))
Ihydrograph <- approxfun(1:101, inflow)
Routing(Ihydrograph, k = 20, m = 1, T = 100, plotit = TRUE, return.values = FALSE)



############################################
# Influence of k

# Wrap Routing as a function of k

Routing_k <- function(k, Ihydrograph, m, T, dt = 1, plotit = TRUE, return.values = FALSE){
Routing(Ihydrograph, k, m, T, dt = 1, plotit = plotit, return.values = return.values )
}
k.seq <- c(1, 5, 10, 15, 20, 50)
x <- lapply(k.seq, FUN = Routing_k, Ihydrograph = Ihydrograph, m = 0.8, T = 100, dt = 1, plotit = FALSE, return.values = TRUE)
x1 <- do.call(cbind, x)

plot(Ihydrograph(1:100), type = 'l', col = 'blue', las = 1, ylab = 'flow', xlab = 'Time step') # Inflow hydrograph
matlines(x1)
legend('topright', legend = k.seq, col = 1:6, lty = 1:5, bty = 'n' )

1 thought on “Routing in RORB”

  1. Pingback: Routing in RORB – II | tonyladson

Leave a comment